CapacitĂŠ des batteries acide-plomb
DĂŠfinition
La capacitÊ d'une batterie est la quantitÊ d'Ênergie Êlectrique qu'elle est capable de restituer après avoir reçue une charge complète, pour un courant de dÊcharge donnÊ, une tempÊrature et une tension d'arrêt dÊfinies. Chose Êtonnante mais bien rÊelle, la capacitÊ de la batterie dÊpend du courant de dÊcharge : la capacitÊ diminue lorsque le courant de dÊcharge augmente.
La capacitÊ s'exprime thÊoriquement par l'unitÊ d'Ênergie wattheures (Wh). Usuellement, on utilise l'unitÊ ampèreheure (Ah). Cette dernière n'est certes pas une unitÊ d'Ênergie, mais il suffit de la multiplier par la tension (fixe) de la batterie pour obtenir des wattheures (Watt = Ampère à Volt).
La capacitĂŠ dâune batterie se note CTd oĂš Td reprĂŠsente une durĂŠe en heures. Ainsi CTd = X signifie que la batterie peut dĂŠlivrer un courant dâintensitĂŠ X/Td (en ampère) pendant une durĂŠe Td (en heure). Autrement dit, en maintenant un tel courant (X/Td), la dĂŠcharge sera atteinte au bout de la durĂŠe Td.
Ainsi, en notant :
- Td : l'autonomie de la batterie (son temps de dĂŠcharge).
- CTd : la capacitĂŠ de la batterie associĂŠe Ă lâautonomie Td.
- ITd : le courant de dĂŠcharge de la batterie associĂŠe Ă lâautonomie Td.
Exemples
1) C6 = 66 Ah signifie que la batterie peut fournir un courant de 66/6=11 A pendant 6 heures avant dÊcharge complète.
Attention : cela ne signifie pas que la batterie peut fournir 22 A pendant 3 heures, ou bien 5.5 A pendant 12 heures. Il nây a pas de relation de linĂŠaritĂŠ (voir la loi de Peukert).
2) C20 = 200 Ah signifie que la batterie peut fournir un courant de 200/20=10 A pendant 20 heures avant dÊcharge complète.
Attention : cela ne signifie pas que la batterie peut fournir 20 A pendant 10 heures, ou bien 5 A pendant 40 heures. Il nây a pas de relation de linĂŠaritĂŠ (voir la loi de Peukert).
CapacitĂŠ nominale
Il existe donc une infinitĂŠ de capacitĂŠ associĂŠ Ă une batterie. Chacune dâentre elles ĂŠtant associĂŠe Ă une durĂŠe de dĂŠcharge.
Afin de comparer les batteries entre elle, la profession a dĂŠcidĂŠ de dĂŠfinir une capacitĂŠ nominale, notĂŠ CN. Selon le domaine d'application de la batterie, une valeur nominale est clairement dĂŠfinie. Cette capacitĂŠ nominale, CN est indiquĂŠ sur les fiches techniques de batteries
Les valeurs utilisĂŠes habituellement par les constructeurs sont les suivantes :
| Domaine d'application | CapacitĂŠ nominale courante |
|---|---|
| Batteries de traction | CN = C5 Pour les voitures ĂŠlectriques, CN = C1 |
| Batteries stationnaires | CN = C10 Pour les applications photovoltaĂŻques, CN = C120 |
| Batteries de dĂŠmarrage | CN = C20 |
Loi de Peukert
Nous venons de voir que la capacitĂŠ, le courant de dĂŠcharge et lâautonomie de la batterie sont trois grandeurs ĂŠtroitement liĂŠes. Par dĂŠfinition de la capacitĂŠ, nous avons ĂŠtabli la relation suivante : CTd = ITd × Td.
La loi de Peukert correspond Ă une deuxième relation liant lâautonomie Td et le courant de dĂŠcharge ITd de la batterie.
=> Constat expĂŠrimentale de la loi de Peukert
ConsidÊrons 5 batteries, numÊrotÊes de 1 à 5, prÊsentant ses capacitÊs nominales C10 respectivement Êgales à 132 Ah, 220 Ah, 325 Ah, 469 Ah et 700 Ah. Puis, mesurons expÊrimentalement leurs capacitÊs pour diffÊrents courants de dÊcharge, et traçons les donnÊes sur un graphe :
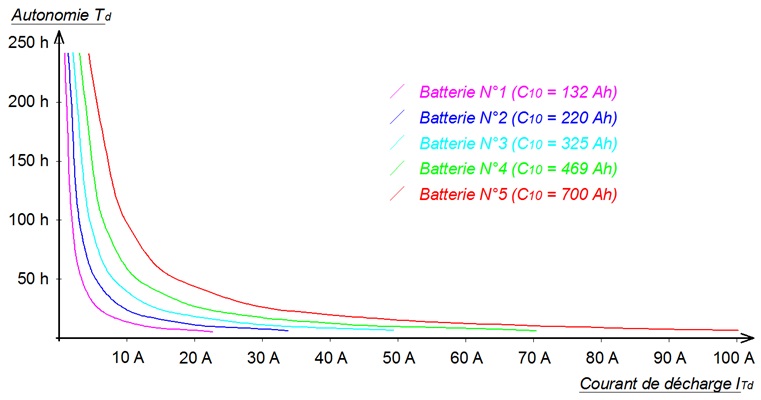
Evolution de lâautonomie en fonction du courant de dĂŠcharge
Au regard de ces courbes, on constate (ĂŠvidemment) que :
- l'autonomie diminue lorsque que le courant de dĂŠcharge diminue,
- la batterie Ă la plus forte capacitĂŠ nominale prĂŠsente une meilleure autonomie.
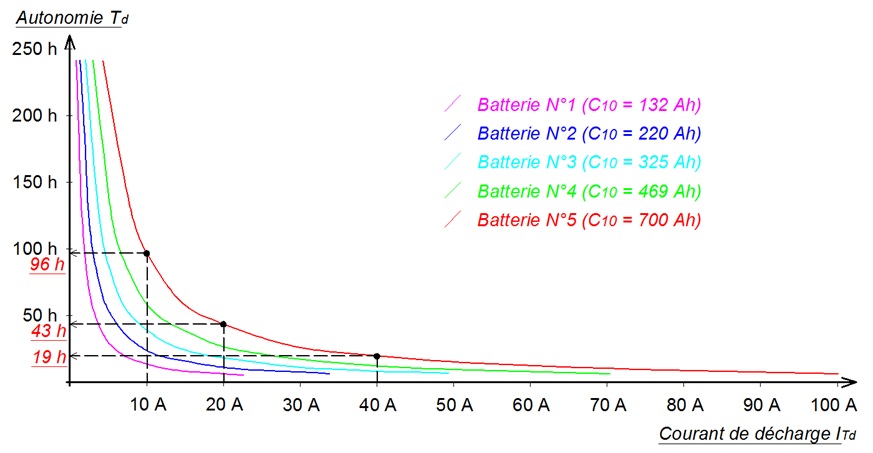 IntĂŠressons-nous maintenant Ă la batterie N°5. Nous observons que l'autonomie pour un courant de dĂŠcharge de 10 A est de 96 h. Le bon sens nous pousse Ă penser que si on double le courant de dĂŠcharge (20 A), on diminue de moitiĂŠ l'autonomie (48 h). Or, ce n'est ce qui est constatĂŠ expĂŠrimentalement. Ainsi qu'illustrĂŠ sur le graphique ci-contre, avec un courant de dĂŠcharge de 20 A, l'autonomie est de 43 h; l'autonomie a ĂŠtĂŠ divisĂŠ 2,23. De mĂŞme, avec un courant multipliĂŠ par 4 (40 A), l'autonomie est divisĂŠe par 5 et non pas par 4.
IntÊressons-nous maintenant à la batterie N°5. Nous observons que l'autonomie pour un courant de dÊcharge de 10 A est de 96 h. Le bon sens nous pousse à penser que si on double le courant de dÊcharge (20 A), on diminue de moitiÊ l'autonomie (48 h). Or, ce n'est ce qui est constatÊ expÊrimentalement. Ainsi qu'illustrÊ sur le graphique ci-contre, avec un courant de dÊcharge de 20 A, l'autonomie est de 43 h; l'autonomie a ÊtÊ divisÊ 2,23. De même, avec un courant multipliÊ par 4 (40 A), l'autonomie est divisÊe par 5 et non pas par 4.Nous venons de mettre en Êvidence une propriÊtÊ importante des batteries, à savoir que l'autonomie et le courant de dÊcharge ne sont pas liÊs par une relation linÊaire.
Pour les 5 batteries ĂŠtudiĂŠes, nous pouvons tenter d'ĂŠtablir la relation entre l'autonomie Td et le courant de dĂŠcharge ITd :
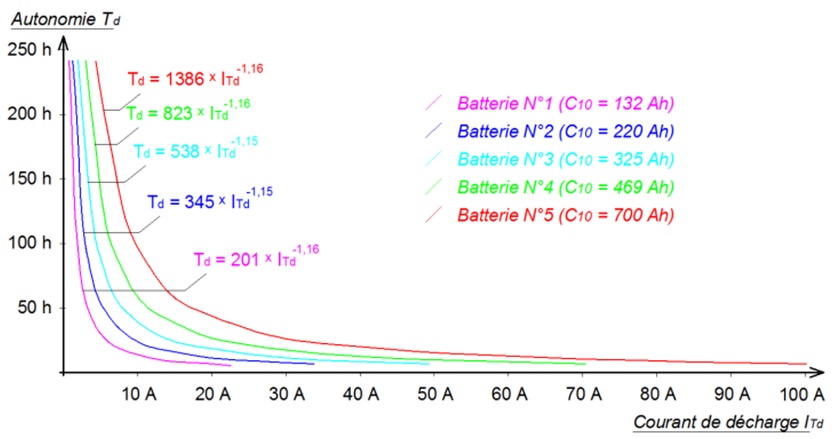 Nous constatons que pour chacune des 5 batteries ĂŠtudiĂŠes, l'autonomie peut s'ĂŠcrire sous la forme suivante : Td=Cp / ITdn.
Nous constatons que pour chacune des 5 batteries ĂŠtudiĂŠes, l'autonomie peut s'ĂŠcrire sous la forme suivante : Td=Cp / ITdn. Cette relation peut s'ĂŠcrire aussi sous cette forme : Cp = ITdn Ă Td.
OÚ les paramètres Cp et n sont des paramètres spÊcifiques à chaque batterie.
A travers cette ĂŠtude, nous avons donc fait ressortir une relation remarquable : Cp = ITdn Ă Td.
Cette relation a ĂŠtĂŠ dĂŠcouverte en 1897 par le scientifique allemand Peukert. Elle est nommĂŠe la loi de Peukert. Cette loi est valable pour tous les accumulateurs au plomb.
Les paramètres Cp et n sâappellent respectivement la capacitĂŠ de Peukert et lâexposant de Peukert. Ils sont propres Ă une batterie. On notera que c'est le coefficient n qui induit la non-linĂŠaritĂŠ entre l'autonomie et le courant de dĂŠcharge. En effet, si n=1, alors la relation de Peukert devient Td = Cp / ITd (si on double le courant de dĂŠcharge, alors on diminue de moitiĂŠ l'autonomie). NĂŠanmoins, le cas n=1 n'existe pas dans la rĂŠalitĂŠ, et ce coefficient vaut plutĂ´t entre 1,15 et 1,25 selon les batteries.
InterprĂŠtation physique de la capacitĂŠ de Peukert Cp
Physiquement, la capacitĂŠ de Peukert est ĂŠgale Ă la capacitĂŠ de la batterie pour un courant de dĂŠcharge de 1 A. Ainsi, pour une batterie donnĂŠe, la dĂŠtermination de la constante de Peukert sâeffectue de la façon suivante :
- On impose un courant de dĂŠcharge de ITd=1 A
- On mesure lâautonomie Td.
- On calcule la capacitĂŠ CTd associĂŠe par la formule CTd=ITdĂTd (avec ITd=1 A et Td la valeur mesurĂŠe)
- la constante de Peukert Cp est alors ĂŠgale Ă la capacitĂŠ prĂŠcĂŠdemment calculĂŠe.
En considĂŠrant un temps de dĂŠcharge Td = 10 heures, on obtient les relations suivantes :
En combinant les deux relations, on obtient :
Cp = C10n × 101-n
C10 = (Cp × 10n-1)1/n
La constante de Peukert est donc un indicateur de la capacitĂŠ nominale de la batterie. Plus Cp est grand, plus la capacitĂŠ nominale de lâaccumulateur est importante, et par suite, plus lâautonomie sera importante ĂŠgalement.
InterprĂŠtation physique de l'exposant de Peukert n
Lâexposant de Peukert permet de quantifier la dĂŠpendance de la capacitĂŠ par rapport au courant de dĂŠcharge. Lâexposant de Peukert est toujours supĂŠrieur ou ĂŠgale Ă 1. Plus n est grand, moins la batterie est performante pour des courants de dĂŠcharge forts.
Sur le graphe ci-dessous, avec n=1, la batterie prĂŠsente une autonomie de 5 heures sous un courant de dĂŠcharge de 40 A. Avec n=1.2, la batterie pourra dĂŠbiter 20 A seulement pour la mĂŞme autonomie (5 heures). Une batterie idĂŠale prĂŠsente un exposant de Peukert n=1. Les fabricants de batterie essaient de se rapprocher de 1. Aujourdâhui, la valeur typique de n est de lâordre de 1.15.
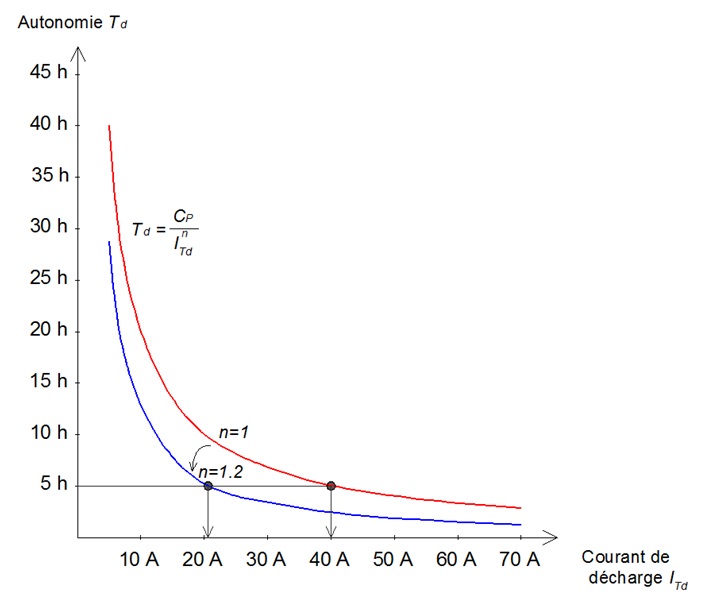
Influence de lâexposant de Peukert sur lâautonomie de la batterie et le courant de dĂŠcharge (CP = 200 Ah).
La dĂŠtermination expĂŠrimentale de lâexposant de Peukert peut sâeffectuer selon le procĂŠdĂŠ suivant :
- On rĂŠalise une première expĂŠrience oĂš on impose un courant de dĂŠcharge ITd,1. Pour ce courant de dĂŠcharge, on mesure lâautonomie associĂŠe Td,1.
- Puis on rĂŠalise une deuxième expĂŠrience semblable mais avec un courant de dĂŠcharge ITd,2. Pour ce courant de dĂŠcharge, on mesure lâautonomie associĂŠe Td,2.
- Ensuite, en appliquant la loi de Peukert, on a : Cp = ITd,1n Ă Td,1 = ITd,2n Ă Td,2 car Cp est une constante qui est spĂŠcifique Ă la batterie et donc indĂŠpendante du courant de dĂŠcharge.
- Il convient donc ensuite de rĂŠsoudre lâĂŠquation ITd,1n Ă Td,1 = ITd,2n Ă Td,2, n ĂŠtant lâinconnue. On trouve alors : n = ln(Td,2/Td,1) / ln(ITd,1/ITd,2).
Justification chimique de la Loi de Peukert
La loi de Peukert permet de quantifier la dĂŠpendance de la capacitĂŠ de la batterie par rapport au courant de dĂŠcharge. Qualitativement, on la tendance suivante :
| Cause | ConsĂŠquence |
|---|---|
| Courant de dĂŠcharge augmente | CapacitĂŠ diminue Autonomie diminue |
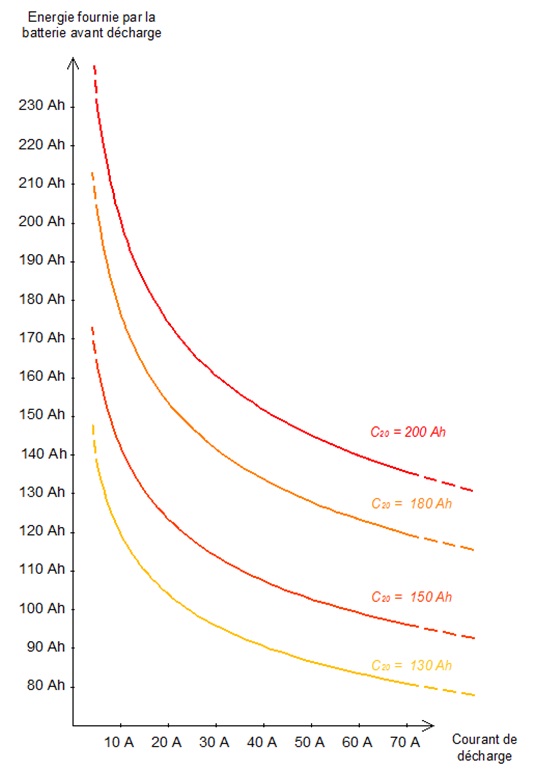 La dĂŠcharge est donc dâautant plus efficace que le courant de dĂŠcharge est faible. Comme la capacitĂŠ reprĂŠsente la quantitĂŠ dâĂŠnergie que peut fournir une batterie, on en dĂŠduit que plus le courant de dĂŠcharge est important, moins la batterie fournie dâĂŠnergie.
La dĂŠcharge est donc dâautant plus efficace que le courant de dĂŠcharge est faible. Comme la capacitĂŠ reprĂŠsente la quantitĂŠ dâĂŠnergie que peut fournir une batterie, on en dĂŠduit que plus le courant de dĂŠcharge est important, moins la batterie fournie dâĂŠnergie.LâĂŠnergie ĂŠlectrique que peut fournir la batterie suit donc une courbe dĂŠcroissante ainsi quâillustrĂŠ ci-contre.
Par consĂŠquent, lorsque le courant de dĂŠcharge augmente, il y a moins d'ĂŠnergie disponible. On est alors en droit de se poser la question : oĂš est passĂŠe l'ĂŠnergie initiale de la batterie ?
Un ĂŠlĂŠment de rĂŠponse vient du fait que lorsque le courant de dĂŠcharge est important, la concentration en rĂŠactif au sein de lâĂŠlectrolyte au voisinage des ĂŠlectrodes diminue Ă un rythme plus soutenue que celui du phĂŠnomène de diffusion des ions. Or, le phĂŠnomène diffusion au sein de lâĂŠlectrolyte permet lâapport dâacide sulfurique nĂŠcessaire aux rĂŠactions chimiques. Ainsi, on atteint le niveau de dĂŠcharge plus rapidement quand a un courant plus ĂŠlevĂŠ. Mais si on attend, on constatera que la batterie se recharge car la diffusion des rĂŠactifs comble le vide local au voisinage des ĂŠlectrodes.
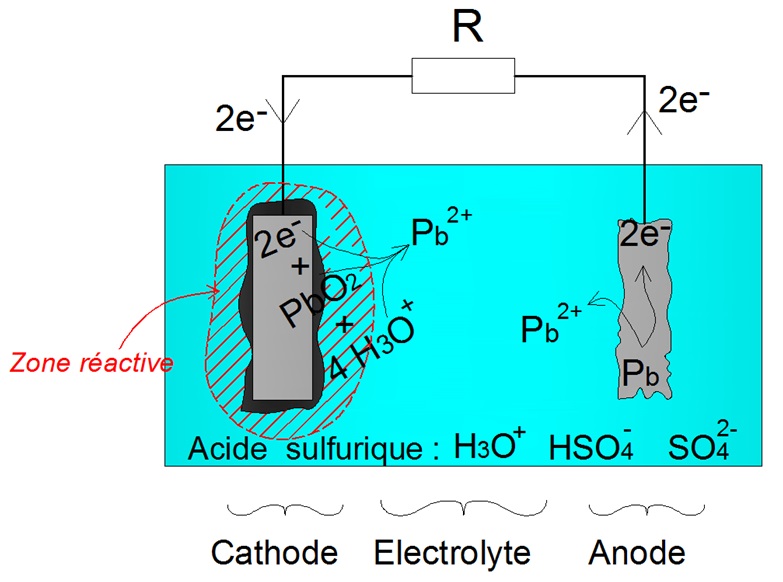 La zone hachurĂŠe rouge, sur le schĂŠma ci-contre, est la zone dans laquelle lâacide sulfurique (H3O+) est consommĂŠ lors de la dĂŠcharge. Plus le courant de dĂŠcharge augmente, plus la concentration dâacide sulfurique diminue au voisinage de la cathode. Lorsquâil nây plus assez dâacide sulfurique au voisinage de lâĂŠlectrode, la batterie ne fournit plus de courant : elle est considĂŠrĂŠe comme dĂŠchargĂŠ. Il faut attendre un certain temps pour les ions H30+ migrent Ă nouveau au voisinage de la cathode.
La zone hachurĂŠe rouge, sur le schĂŠma ci-contre, est la zone dans laquelle lâacide sulfurique (H3O+) est consommĂŠ lors de la dĂŠcharge. Plus le courant de dĂŠcharge augmente, plus la concentration dâacide sulfurique diminue au voisinage de la cathode. Lorsquâil nây plus assez dâacide sulfurique au voisinage de lâĂŠlectrode, la batterie ne fournit plus de courant : elle est considĂŠrĂŠe comme dĂŠchargĂŠ. Il faut attendre un certain temps pour les ions H30+ migrent Ă nouveau au voisinage de la cathode.
Effet de la tempĂŠrature sur la capacitĂŠ
La tempĂŠrature est un catalyseur des rĂŠactions chimiques : une augmentation de 10°C double les cinĂŠtiques des rĂŠactions. Ainsi, lâaugmentation de la tempĂŠrature permet une amĂŠlioration de la capacitĂŠ de la batterie. On introduit donc un coefficient de tempĂŠrature KT(C) liĂŠ Ă lâĂŠvolution de la capacitĂŠ en fonction de la tempĂŠrature de la batterie. Comme les fabricants indiquent la capacitĂŠ pour une tempĂŠrature de 20°C, le coefficient KT(C) est pris ĂŠgal Ă 1 pour cette tempĂŠrature. Les valeurs des coefficients de tempĂŠrature de la capacitĂŠ sont donnĂŠs ci-dessous Ă titre indicatif :
| TempÊrature | -20 °C | -10 °C | 0 °C | 10 °C | 20 °C | 30 °C | 40 °C | 50 °C |
|---|---|---|---|---|---|---|---|---|
| C20 | 0.63 | 0.74 | 0.85 | 0.94 | 1 | 1.05 | 1.1 | 1.15 |
| C10 | 0.58 | 0.68 | 0.81 | 0.91 | 1 | 1.04 | 1.09 | 1.13 |
| C4 | 0.55 | 0.67 | 0.80 | 0.90 | 1 | 1.07 | 1.15 | 1.22 |
| Coefficient de tempĂŠrature de la capacitĂŠ de la batterie â Colonne verte : tempĂŠrature de rĂŠfĂŠrence, 20°C | ||||||||
Exemple de lecture du tableau
La capacitĂŠ C20, T=-10°C Ă -10°C est ĂŠgale Ă 0.74 multipliĂŠ par la capacitĂŠ C20, T=20°C Ă 20°C. Soit : C20, T=-10°C = 0.74 Ă C20, T=20°C. En dâautres mots : Ă -10 °C, la capacitĂŠ C20 vaut 74% de la capacitĂŠ C20 Ă 20°C.
Remarque
Attention cependant, si lâaugmentation de la tempĂŠrature favorise la capacitĂŠ de la batterie, la rapiditĂŠ dâautodĂŠcharge est ĂŠgalement accrue.

